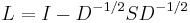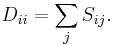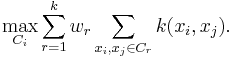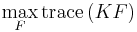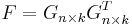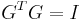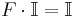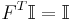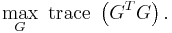Spectral clustering

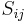Given a set of data points A, the similarity matrix may be defined as a matrix S, where S_{ij} represents a measure of the similarity between points 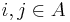i, j\in A. Spectral clustering techniques make use of the spectrum of the similarity matrix of the data to perform dimensionality reduction for clustering in fewer dimensions.

Contents

Algorithms

One such technique is the normalized cuts algorithm or Shi–Malik algorithm introduced by Jianbo Shi and Jitendra Malik,[1] commonly used for image segmentation. It partitions points into two sets 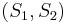(S_1,S_2) based on the eigenvector v corresponding to the second-smallest eigenvalue of the Laplacian matrix

L = I - D^{-1/2}SD^{-1/2} \,

of S, where D is the diagonal matrix

D_{ii} = \sum_j S_{ij}.

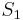This partitioning may be done in various ways, such as by taking the median m of the components in v, and placing all points whose component in v is greater than m in S_1, and the rest in 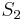S_2. The algorithm can be used for hierarchical clustering by repeatedly partitioning the subsets in this fashion.

A related algorithm is the Meila–Shi algorithm[2], which takes the eigenvectors corresponding to the k largest eigenvalues of the matrix 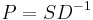P = SD^{-1} for some k, and then invokes another algorithm (e.g. k-means) to cluster points by their respective k components in these eigenvectors.

Relationship with k-means

The kernel k-means problem is an extension of the k-means problem where the input data points are mapped non-linearly into a higher-dimensional feature space via a kernel function 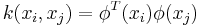k(x_i,x_j) = \phi^T(x_i)\phi(x_j). The weighted kernel k-means problem further extends this problem by defining a weight 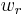w_r for each cluster as the reciprocal of the number of elements in the cluster,

\max_{C_i} \sum_{r=1}^k w_r \sum_{x_i,x_j \in C_r} k(x_i,x_j).

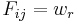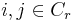Suppose F is a matrix of the normalizing coefficients for each point for each cluster F_{ij} = w_r if i,j \in C_r and zero otherwise. Suppose K is the kernel matrix for all points. The weighted kernel k-means problem with n points and k clusters is given as,

\max_{F} \operatorname{ trace } \left(KF\right)

such that,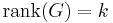

F = G_{n\times k}G_{n\times k}^T
G^TG = I

such that \text{rank}(G) = k. In addition, there are identity constrains on F given by,

F\cdot \mathbb{I} = \mathbb{I}

where \mathbb{I} represents a vector of ones.

F^T\mathbb{I} = \mathbb{I}

This problem can be recast as,

\max_G \text{ trace }\left(G^TG\right).

This problem is equivalent to the spectral clustering problem when the identity constraints on F are relaxed. In particular, the weighted kernel k-means problem can be reformulated as a spectral clustering (graph partitioning) problem and vice-versa. The output of the algorithms are eigenvectors which do not satisfy the identity requirements for indicator variables defined by F. Hence, post-processing of the eigenvectors is required for the equivalence between the problems[3].

References

  1. ^ Jianbo Shi and Jitendra Malik, "Normalized Cuts and Image Segmentation", IEEE Transactions on PAMI, Vol. 22, No. 8, Aug 2000.
  2. ^ Marina Meilă & Jianbo Shi, "Learning Segmentation by Random Walks", Processing Systems 13 (NIPS 2000), 2001, pp. 873–879.
  3. ^ Dhillon, I.S. and Guan, Y. and Kulis, B. (2004). "Kernel k-means: spectral clustering and normalized cuts". Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining. pp. 551--556. 

See also